贪食蛇 AI 初等套路

—— 前言 ——

贪食蛇 AI 是入门人工智能的第二个练手项目（刚开始打算写俄罗斯方块，看了 El-Tetris 那个实现方法，感觉太没挑战性直接跳过了）。不得不承认的是除了 AI 设计上的严谨性，“吃满整块画布” 也得靠运气。除了俄罗斯人制作的牛逼 GIF（我们至今无从知道实现细节）以外，没有一段代码可以做到一个洞也不留的。这背后一定有一些更深刻的原理值得探讨……

Auto Snake

鄙人设计的一个不算太牛逼的版本（画面周围有 margins，有效区域只有 200x160 像素）

—— 实现细节 ——

【启发式路径搜索】

深度优先 (DFS) 和广度优先 (BFS) 遍历，没学过 CS 的人从名字都可以理解它们的原理。这两种算法被用于没有地形的游戏中，可以计算出 “仅限于俯视图视角的最优解”。对于需要考虑第三个维度的情形（例如：山脉），地图中相邻节点之间的移动代价并不相等，深搜和广搜就不适用了。这种情形下你必须用 Dijkstra，它考虑了从起始点出发、到达地图上每一点的移动代价，并提高了搜索效率。

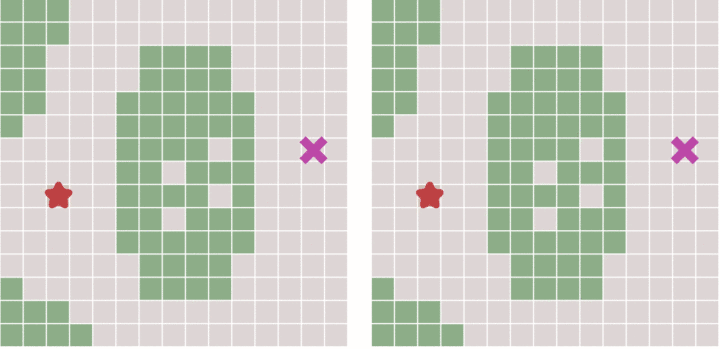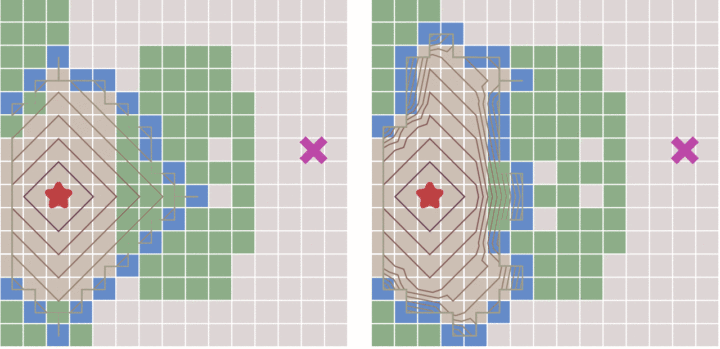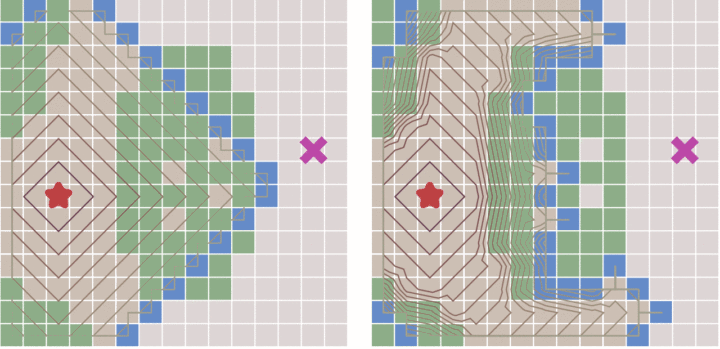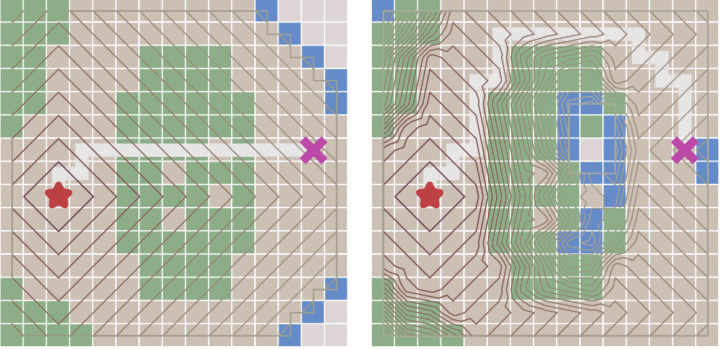
BFS vs. Dijkstra

广度优先遍历和 Dijkstra 在同一张带有地形的地图上的搜索进程，转自 https://zhuanlan.zhihu.com/p/54510444

我相信有很多喜欢上 CS 这个专业的人，都或多或少从游戏中获得过灵感。在 id Software 早期的几部作品里，经常会见到玩家与大量的 NPC 交火，犹如一个 “孤胆英雄” 一般，独自一人对抗一群怪兽（或者是德军 officers）。在当时只有 16 MB 内存的电脑上，却几乎很少有卡顿的感觉，这是一件非常不可思议的事情。现在回想起来，这种剧情太不真实。但如果深入剖析，除了分辨率低以外，原因其实有很多。虽然说的不是一部游戏，它们的算法都是一样的。

之所以那时的游戏 NPC 数量比现在的游戏多，是因为 3D 图形技术刚在起步，该游戏的制作者 John Carmack 在程序中应用了伪 3D 投影 —— 按照我的理解，被遮挡住的墙壁和物体不需要渲染，也不需要计算光照和阴影上的变化（明暗面主要通过 sprites 体现出来），就可以把更多的系统资源用来做其它处理。又由于玩家的位置是不断更新中的，需要一种高效的算法为每一个移动中的 NPC 实时地规划移动路线。

受到了这种设计的启发，在贪食蛇 AI 里，尽管食物的位置在刷新前是固定的，随着蛇的行进，蛇尾会让出更多的空间，行为策略也要做出相应的调整（有时需要把蛇尾设为寻路目标）。于是乎轨迹需要在每一步移动后重新规划。

A-Star 发表于 1968 年，被广泛地应用于游戏中电脑所控制的角色 (NPC)，是最高效、使用最灵活的寻路算法 [Nosrati et al., 2012]。我们都有这样的经历，在迷宫里，无论你藏在哪个角落，那些（上一轮与你交火但还没被干掉的）NPC 们会自动地寻找到你。只有 boss 的 AI 是经过专门设计的。

根据启发函数 (F=G+H) 所计算出的优先级，A-Star 算法对每一步移动中下一个要遍历的节点 (next_move) 进行排序，F 小的优先选择。其中 G 为从起始点出发、到达 next_move 的移动代价，H 是以 next_move 为起始点、到达终点的距离预估。对于距离的估算有以下三种方法：

如果游戏中只允许朝上下左右四个方向移动，则使用曼哈顿距离
如果游戏中允许朝八个方向移动，则使用对角距离
如果游戏中允许朝任何方向移动，则使用欧几里得距离

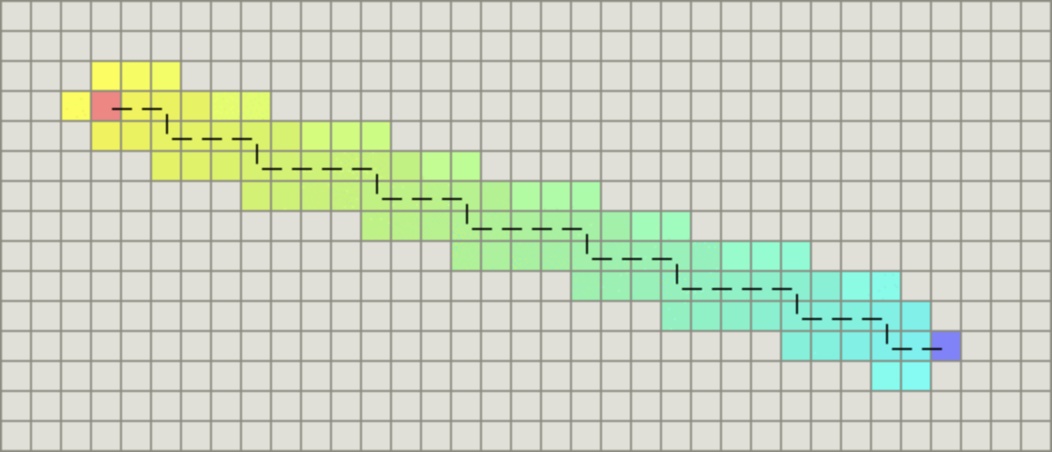
Manhattan

曼哈顿距离的计算，转自 https://zhuanlan.zhihu.com/p/54510444

在每一次调用中，A-Star 优先根据节点的 H 做选择。若多个节点的 H 相等，则根据 G 来选，此时 A-Star 和 Dijkstra 工作原理相同。不用说大家也知道，程序中一旦涉及路径规划问题，比较明智的做法是直接编写 A-Star 算法的代码。因为当强制参数 H=0 时，就可以当成 Dijkstra 来用。

对节点进行排序的数据结构，称为优先级队列 (Priority-Queue)。考虑到贪食蛇这个游戏里，每一步移动最多只有三个方向可供选择，初等的写法对效率的影响可以忽略。我们可以用匿名函数 lambda 语法实现等效的优先级排序操作：

def manhattan(node_1, node_2):
    """Cost computation for the case that
    only four directions' moves are permitted."""
    dist_x = abs(node_2.x - node_1.x)
    dist_y = abs(node_2.y - node_1.y)
    return dist_x + dist_y

def astar(maze, start, current, end, visited=[], path=[]):
    """Subroutine for finding the optimum path in a maze
    by computing the cost of each move."""
    if current == end:
        return visited, path

    # enumerate unvisited connected neighbors
    choices = [N for N in maze.GetNeighbors(current) \
        if N not in visited]

    # when two nodes have the same H
    # the one with the smaller G comes first
    choices.sort(key=lambda c: manhattan(start, c))
    choices.sort(key=lambda c: manhattan(c, end))

    for next_move in choices:
        visited.append(next_move)
        path.append(next_move)
        v_final, p_final = \
            astar(maze, start, next_move, end, visited, path)
        if p_final is not None:
            return v_final, p_final
        else:
            path.pop()

    return visited, None

【后台演算方法】

前面提到的最短路径和后面将要讨论的最长路径都是最优解比较确定的问题。随机路线相比之下不确定度比较大，需要一条虚拟的蛇（深拷贝）去探路以确保安全（后台演算）。在没查过前人解法的情况下，我首先想到的就是这种策略。

在贪食蛇这个游戏里，很多导致 Game Over 的走法很难通过向前一步的移动预测出来。蛇和墙或者蛇的某一段与平行的另一段之间只留下一条路的距离，进入后没有空间掉头返回，只有撞墙或者撞自己… 这种对真实玩家非常容易避免的情形，对 AI 来说却很难处理。随着蛇长度的增加，难以考虑进去的特征点越来越多，会给 AI 的设计带来难度。倘若把所有的形态都考虑进去，这样的 AI 分支太多，想必代码也不美观。

于是乎很自然地想到从当前状态出发，把后面几步的事件在后台推演出来，先派一条虚拟的蛇去试探（不需要显示在屏幕上），看哪些走法可能导致 Game Over 的结局。如果某一种走法没有直接地导致 Game Over，但算法判断出这种走法具有一定危险（蛇尾与身体围成的区域），也将它赋予更低的优先级。

这种设计，借鉴了五子棋和国际象棋 AI 里的博弈树思想。大多数算法书里，都用 Tic-Tac-Toe 这个游戏来演示博弈树原理。经典的汉诺塔问题可以用一个三角形的 configuration graph 表示出来，每一个节点存储一种状态；两个节点之间用一条边连接，当且仅当两种状态之间可以通过一步移动相互转化 [Romik, 2006; Cohen, 2008; Berend, 2012]，实际上也是一种博弈树的原理。

def chaseTail(snake, canvas, food):
    """Forwards the snake one step towards its the tail."""
    fake_snake = snake[:]
    fake_canvas = resetCanvas(fake_snake, canvas, food)
    end_idx = fake_snake[-1].x + fake_snake[-1].y * MATRIX_W
    fake_canvas[end_idx] = FOODNUM
    v_food = fake_snake[-1]
    food_idx = food.x + food.y * MATRIX_W
    fake_canvas[food_idx] = MAXLENGTH
    result, refresh_tcanvas = runAstar(fake_snake, v_food, fake_canvas)
    fake_canvas = refresh_tcanvas
    fake_canvas[end_idx] = MAXLENGTH
    path = longestPath(fake_snake, fake_canvas)
    return path

def virtualMove(snake, canvas, food):
    """Forwards the snake one step virtually."""
    fake_snake = snake[:]
    fake_canvas = canvas[:]
    reset_tcanvas = resetCanvas(fake_snake, fake_canvas, food)
    fake_canvas = reset_tcanvas
    eaten = False
    while not eaten:
        refresh_tcanvas = runAstar(fake_snake, food, fake_canvas)[1]
        fake_canvas = refresh_tcanvas
        next_move = shortestPath(fake_snake, fake_canvas)
        snake_coords = fake_snake[:]
        fake_snake.insert(0, getHeadCoords(snake_coords, next_move))
        if fake_snake[0] == food:
            reset_tcanvas = resetCanvas(fake_snake, fake_canvas, food)
            fake_canvas = reset_tcanvas
            food_idx = food.x + food.y * MATRIX_W
            fake_canvas[food_idx] = MAXLENGTH
            eaten = True
        else:
            newHead_idx = fake_snake[0].x + fake_snake[0].y * MATRIX_W
            fake_canvas[newHead_idx] = MAXLENGTH
            end_idx = fake_snake[-1].x + fake_snake[-1].y * MATRIX_W
            fake_canvas[end_idx] = CKBBOARD
            del fake_snake[-1]
    return fake_snake, fake_canvas

以上计算中，food_idx = food.x + food.y * MATRIX_W 给出的是从 0 开始计数、从左上角数起的总单元格数目，且 newHead_idx 与 end_idx 的计算同理。该坐标转换方法借鉴了 Al Sweigart 的教程（一个不带 AI 的贪食蛇原版），许多贪食蛇 AI 的代码是从这个版本修改而来的。如有相似，绝无盗用。

我们还需要一个函数 isSafe(target, snake) 来判断目标与蛇头之间的区域是否安全。把完整的算法套路总结如下：

条件一：如果蛇头与食物之间的空间是安全的（没有被身体的其它部分挡住），则使用最短的路径去吃食物 (target = food)
条件二：如果条件一不满足，但是蛇头与尾巴之间存在通路（画布没有被蛇的身体分割为互不相通的区域），则使用尽可能迂回的路线去追自己尾巴 (target = tail)
如果以上两个条件都不满足，设计随机路线让蛇闲逛，同时使用虚拟的蛇去探路以避免闲逛的蛇进入死路，直到以上两个条件至少有一个重新出现

以上条件检查必须在每一步移动后重新执行。除了 BFS、DFS 和 A-Star 算法，最短路径还可以用最佳优先搜索来查找；当所用数据结构为优先队列时，最佳优先搜索的时间复杂度为 O[V+ElogE]。若为有向图，最长路径可以用拓扑排序（一种按照节点的入度对有向图排序的算法，时间复杂度为 O[V+E]）优化后再进行搜索，这要求有向图必须是无环的 [Khan, 2011]。That being said，许多无环图 (simple graphs) 上的算法只需要稍加修改就可以被用于有环图 (multigraphs) 上，或者不修改就能工作。

使用最佳优先搜索提高路径查找的效率很好地体现了贪心算法的思想，我把以上贪食蛇 AI 的套路称为贪心策略。当蛇按照最短路径的走法每向前一步，尽管离 “最短路径” 的目标很远，这一步有效地导致正解的产生，称之为 safe move。由此把问题一步一步地缩小，此乃贪心 + 递归的思路。

【最长路径算法】

设一个无向图中有 N 个顶点，若所有顶点的度数大于等于 N/2，则哈密顿回路一定存在（N/2 指的是 ⌈N/2⌉，向上取整）。

需满足的必要条件为：

设图 G=<V, E> 是哈密顿图，则对于 v 的任意一个非空子集 S，若以 |S| 表示 S 中元素的数目，G-S 表示 G 中删除了 S 中的点以及这些点所关联的边后得到的子图，则 W(G-S)<=|S| 成立。其中 W(G-S) 是 G-S 中联通分支数。

玩过贪食蛇的人都懂，即使是蛇头与尾巴之间没有身体的其它部分挡住，chaseTail() 也要使用尽可能迂回的路线，不可以直接朝着尾巴走，这便是我们使用最长路径的原因。在贪食蛇 AI 里引入图论概念是整套算法流程的关键，哈密顿路径的使用大大提高了 “吃满整块画布” 的成功概率，其基本要求是画布的长和宽至少有一个是偶数（取决于盘绕方向）。考虑到实际情况中，无法控制蛇的盘绕方向，所以把两者都设为偶数，至少从理论上确保哈密顿路径是存在的。

在鄙人第一个版本 (Tortoise.automate) 里，画布上所有未占用的格子首先被转化成一个方便存储图结构的递归系统。NumPy 虽然可以遍历，却没有显式地表示出每一个节点与其相邻节点之间的关系。所以从 Computer Science 的角度来说，我们认为这玩意儿并不好用。真有需求进一步优化，那要针对所需要解决的问题选择最合适的数据结构，链表对频繁插入和删除的操作比 NumPy 效率更高。

import collections

class UndirectedGraph(collections.Sequence):
    """A data structure that allows
    bidirectional traversals."""
    def __init__(self, nodes=None):
        if nodes is None:
            nodes = []
        self.__nodes = nodes

    def InsertNode(self, node):
        if node not in self.__nodes:
            self.__nodes.append(node)

    def __str__(self):
        res = 'Nodes:\n'
        for node in self.__nodes:
            res += (str(node) + '\n')
        return res

g = UndirectedGraph()
g.InsertNode(source)
g.InsertNode(node_1)
g.InsertNode(node_2)
# ...
g.InsertNode(sink)

尽管所用数据结构为无向图类，我们需要对节点 source 和 sink 的 neighbors 属性专门修改，以体现出搜索从 source 开始、到 sink 结束的先后顺序。其中 source 为有向图中入度为 0 的节点；sink 为出度为 0 的节点。节点类的定义如下：

from copy import deepcopy

class Node(object):
    """Data structure for representing
    each cell on the map."""
    def __init__(self, current, neighbors):
        self.__current = current
        self.__neighbors = neighbors

    @property
    def current(self):
        return self.__current  # deepcopy() removed

    @property
    def neighbors(self):
        return self.__neighbors  # deepcopy() removed

    def __eq__(self, other):
        if isinstance(other, Node):
            return self.current == other.current
        else:
            return NotImplemented

    def __repr__(self):
        name    = self.current
        content = self.neighbors
        return '{!r}: {!r}'.format(name, content)

有了上面的定义，每一个节点就包含有自身的坐标和相邻节点的坐标，方便我们实现递归和动态规划。这种表示图的数据结构是实现一切寻路算法的基础，类似于下面两图所展示的例子：

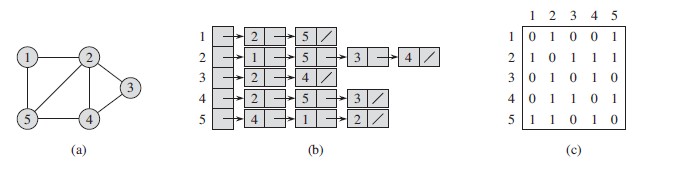
undirected graph

一个无向图及其邻接表与邻接矩阵表示方法

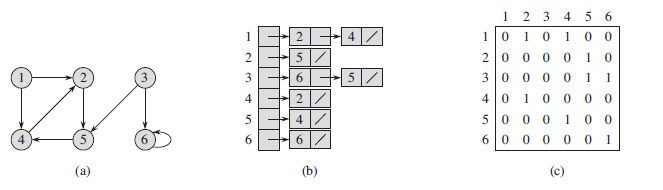
directed graph

一个有向图及其邻接表与邻接矩阵表示方法

一个图的邻接表（即本文使用的方法）表示方法的空间复杂度为 O[V+E]，并与图的无向 / 有向属性无关。邻接矩阵显然比邻接表更消耗内存，但如有必要，可以通过消耗更多的内存来获得效率提升。现在的电脑，内存都足够大了，而运行时间比内存更重要。

最长路径是一个 NP-完全问题 [Gurevich and Shelah, 1987]，没有遍历所有可能，无法判断哪个是最长路径，所以不可能有多项式时间的解法。借助动态规划 [Pearce and Kelly, 2007] 可以把时间复杂度从 O[n(n!)] 优化成 O[(2^n)(n^3)]，n 为节点个数。其基本思路如下：

任意找两个相邻的节点 S 和 T，在其基础上扩展出一条尽量长的没有重复结点的路径。即如果 S 与结点 v 相邻，而且 v 不在路径 S -> T 上，则可以把该路径变成 v -> S -> T，然后 v 成为新的 S。从 S 和 T 分别向两头扩展，直到无法继续扩展为止，即所有与 S 或 T 相邻的节点都在路径 S -> T上。
若 S 与 T 相邻，则路径 S -> T 形成了一个回路。
若 S 与 T 不相邻，可以构造出来一个回路。设路径 S -> T 上有 k+2 个节点，依次为 S, v1, v2, …, vk, T。可以证明存在节点 vi（i 属于 [1, k]），满足 vi 与 T 相邻，且 vi+1 与 S 相邻。找到这个节点 vi，把原路径变成 S -> vi -> T -> vi+1 -> S，即形成了一个回路。
到此为止，已经构造出来了一个没有重复节点的的回路，如果其长度为 N，则哈密顿回路就找到了。如果回路的长度小于 N，由于整个图是连通的，所以在该回路上，一定存在一点与回路之外的点相邻。那么从该点处把回路断开，就变回了一条路径，同时还可以将与之相邻的点加入路径。再按照步骤 1 的方法尽量扩展路径，则一定有新的节点被加进来。接着回到路径 2。

可以证明有向图中，有环状结构与 linear ordering 是一对矛盾的结论，即有环的有向图不可以被 linearly ordered。所以在图论 / 计算机科学里面，我们更关注一类特殊的有向图 —— 有向无环图 (DAG)。只是在贪食蛇这个游戏里面，空闲区域所构造的有向图不可能是无环的。

推荐阅读：Algorithms Unlocked 第五章

【更多设想】

还有哪些算法？

如果你是一个深度学习 / 机器学习 / 大数据的爱好者，卧草那对不起，尽管我也在认真学习，目前没有可行的方法让我对非经典算法产生兴趣。曾经我写过用神经网络 (CNN) 破解数独的程序（原文见此），并讨论了这种方法被用于求约束满足问题 (CSP) 的弊端。数独算错了没有后果，而贪食蛇里面的移动必须非常精准。GitHub 上有人用强化学习 (DQN) 搞了贪食蛇 AI 并统计了终盘时蛇的长度，只能达到其它算法的 40% 左右。之所以这一类方法在围棋和国际象棋中都很牛逼，是因为那些游戏都有一定的容错。对于它在贪食蛇 AI 中的运用，鄙人并不看好。

—— 附录 ——

运行了一波以后，五次得分和覆盖比例与它们的平均值统计：

| Test | Length | Coverage [%] | Ending |
|:----:|:------:|:------------:|:------:|
|   0  | 129    |   89.5833    | **GO** |
|   1  | 142    |   98.6111    | **IL** |
|   2  | 139    |   96.5277    | **IL** |
|   3  | 135    |   93.7500    | **GO** |
|   4  | 138    |   95.8333    | **GO** |
| Mean | 136.6  |   94.8611    |        |

GO: Game Over
IL: Infinite Loop

“完全覆盖” 的定义为 (12x12-1)/(12x12) x 100% = 99.3056%，别忘了食物也要占用一个单元格呢！

以下为各种寻路算法汇总：

Dynamic Window
Grid based algorithms
- Dijkstra（已探讨）
- A* search（已探讨）
- Potential Field algorithm
- Grid based coverage path planning
State Lattice planning
- Biased polar sampling
- Lane sampling
Probabilistic Road-Map (PRM)
Rapidly-Exploring Random Trees (RRT)
- RRT*
- RRT* with reeds-shepp path
- LQR-RRT*
Quintic polynomials planning
Reeds Shepp planning
LQR based path planning
Optimal Trajectory in a Frenet Frame

【参考文献】

Berend, D., Sapir, A., & Solomon, S. (2012). The Tower of Hanoi problem on Pathh graphs. Discrete Applied Mathematics, 160(10-11), 1465-1483.
Cohen, R. (2008). Algorithms and Bounds for Tower of Hanoi Problems on Graphs. Ben Gurion University.
Gurevich, Y., & Shelah, S. (1987). Expected computation time for Hamiltonian path problem. SIAM Journal on Computing, 16(3), 486-502.
Khan, M. (2011). Longest path in a directed acyclic graph (DAG).
Nosrati, M., Karimi, R., & Hasanvand, H. A. (2012). Investigation of the star search algorithms: Characteristics, methods and approaches. World Applied Programming, 2(4), 251-256.
Pearce, D. J., & Kelly, P. H. (2007). A dynamic topological sort algorithm for directed acyclic graphs. Journal of Experimental Algorithmics (JEA), 11, 1-7.
Romik, D. (2006). Shortest paths in the Tower of Hanoi graph and finite automata. SIAM Journal on Discrete Mathematics, 20(3), 610-622.

哈密顿路径、拓扑排序、动态规划和贪心算法的原理

—— 前言 ——

—— 实现细节 ——

—— 附录 ——

CATALOG

FEATURED TAGS

FRIENDS