(接上)
入门深度学习门槛并不高,你不需要自己编写代码来做搜索、寻找最短路径,或是担心内存开销等问题。由于代码的抽象程度高,借助 keras、sklearn 等发展比较完善的工具,哪怕不理解基本原理,仿照别人的代码很快写出像模像样的工程来。随之而来的弊端就是各种不能理解其原理的人(如我)所做的无知假设,这种含糊的态度,只能把自己学渣的地位继续暴露无疑。That said,如果你享受把轮子再造一遍的过程,其原理为 Logistic Regression,这个代码的实现其实并不算难。
据说 “机器学习之父” Arthur Samuel 不太会走跳棋(澄清:此处讨论的不是中国跳棋),他编写了一个训练电脑观察人类走棋步骤、从中获取经验的程序,在当时看来是一个伟大的创举。该程序根据过去获取的数据来预测每一种情形下,求胜概率最高的走法,获得了不错的战绩。与跳棋游戏不同的是,数独只有正误、没有概率高低。用一种图像识别和分类的算法预测数独答案,仅供娱乐,不值得认真。
既然写代码不成问题,问题的难点就成了训练数据从何获取,如果不能,自己编写生成训练数据的程序,效率如何?考虑到磁盘占用与生成题目的用时两点重要因素,我认为题目量在一百万的训练数据比较合适,会不会发生过拟合只有在训练完成后才会知道。
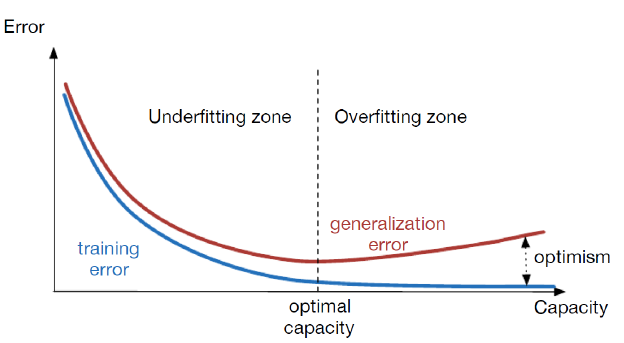
由训练数据过少或过多造成的欠拟合和过拟合现象
多伦多大学的几位作者 [Chiu et al., 2012] 发表了一篇文章,介绍了一种比较严谨的生成数独题目的做法。其大概意思是说:先生成完整的终盘,从中逐个挖去数字;每挖去一个,在同一位置换用别的数字重填,用高效的回溯算法求解,看是否仍然得解;如果是,说明挖去该数字会造成题目存在多解,需另选位置重试;重复以上步骤直到没有更多数字可以被继续剔除。据我所知,数独有不可避免集现象,多解性检查应该在去除数字总数达到 4 时开始,虽然文章里没有提及。
然而这种做法,需要大量的判断和穷举,是为了生成高质量的测试题目(用来测试文章中的并行算法)而提出的,不能用来生成一百万题集。乐观地假设,题目是否存在多解应该对训练效果没有影响。如果这个限定条件可以被去除,生成数独题目的算法就非常高效、简单了,至于是不是没有影响就需要更深层次的讨论。可见如果是为了满足工业生产或工作上的需求,只会写代码而不懂基本原理还没问题,用于学术研究就成了大问题。还是那句话,把自己看得太高是现代人的通病,“想要把轮子造好已经很难了”。
姑且不管这些,先把程序实现了再说。在 yshblog.com 上看到一种做法:从一个预先设计好的起始盘出发 create_base_sudo(),在同一区域内随机挑选两行或两列做互换 random_sudo();互换 50 次后得到一个终盘(即解答),再根据用户所设难度决定挖去数字的个数。该函数平均两毫秒生成一个题目和解答,从速度上可以满足生成大量题目的需求。在经过 50 次打乱以后,所得终盘和起始盘已经相去甚远,换言之没有碰题的可能。至少从原作者的表述看来,期望得到的结果如此。
事情远没有这么简单,还记得前文提到过的等价类的概念,在数独的状态总数 1.96x10^20 中,按照对称性和等价性(例如作者所提在同一区域内交换行和列的做法)可以划分出 5475730538 个类别。大致算上去,每一个等价类约含有 3.58x10^10 种情况。随机挑选行或列进行交换,尽管看起来足够随机,实际上只是在这 3.58x10^10 种情况中变来变去。如果理论上这个算法无法生成所有类型的数独,得到的训练数据就是不完备的,会导致神经网络有偏科。很有可能,原作者要么没指望这个算法可以被应用在深度学习领域,要么没有做这方面的考虑。
修改这个问题其实非常简单,只要对前面写好的回溯法函数稍加修改,变更为 n_queens_rand(),每生成一个候选数字列表做一次打乱(引入随机性);用 n_queens_rand() 来替换原程序里的 create_base_sudo(),再相应地把随机交换行和列的操作从 50 次修改到 7 次就基本上没问题了。由于沿横向、纵向各有三个宫格,于是 C(1,6);从中选择两个进行互换,组合数为 C(2,3);考虑到 (632)^7 = 7.84x10^10,差不多是 3.58x10^10 的两倍那么多,足以得到充分的打乱。
用这种算法生成训练题目,平均每道题用时 7 毫秒,打乱次数从 50 减少到 7 节省的时间可以忽略不计,替换函数 create_base_sudo() 为 n_queens_rand() 所带来的用时增长为 5 毫秒多一点。这个时间比起用回溯法来求解一般的数独题目缩短很多,由此可见提示数字既是线索、也是约束,用回溯法生成题目,比起用回溯法求解数独要快不少。
在排除了以上疑难问题后,很快便编写了这样一个程序,把题目和答案按如下格式存储,难度从一到五随机排布。
1
2
3
4
006780013000000500200400009020...760 546789213879123546213456879324...768
819324756000657189506081423354...310 819324756243657189576981423354...312
078000040640070000300005008400...090 978312645645978312312645978423...291
...
生成一百万题目的用时如下:
1
2
3
Generating quiz 1000000...
Done. File saved as: ./input/models/training.demo.txt
Elapsed time is 7060.032693 seconds.
生成的训练题目中,初始数字的个数分布如下图(纵轴为每一千题目里的出现次数):
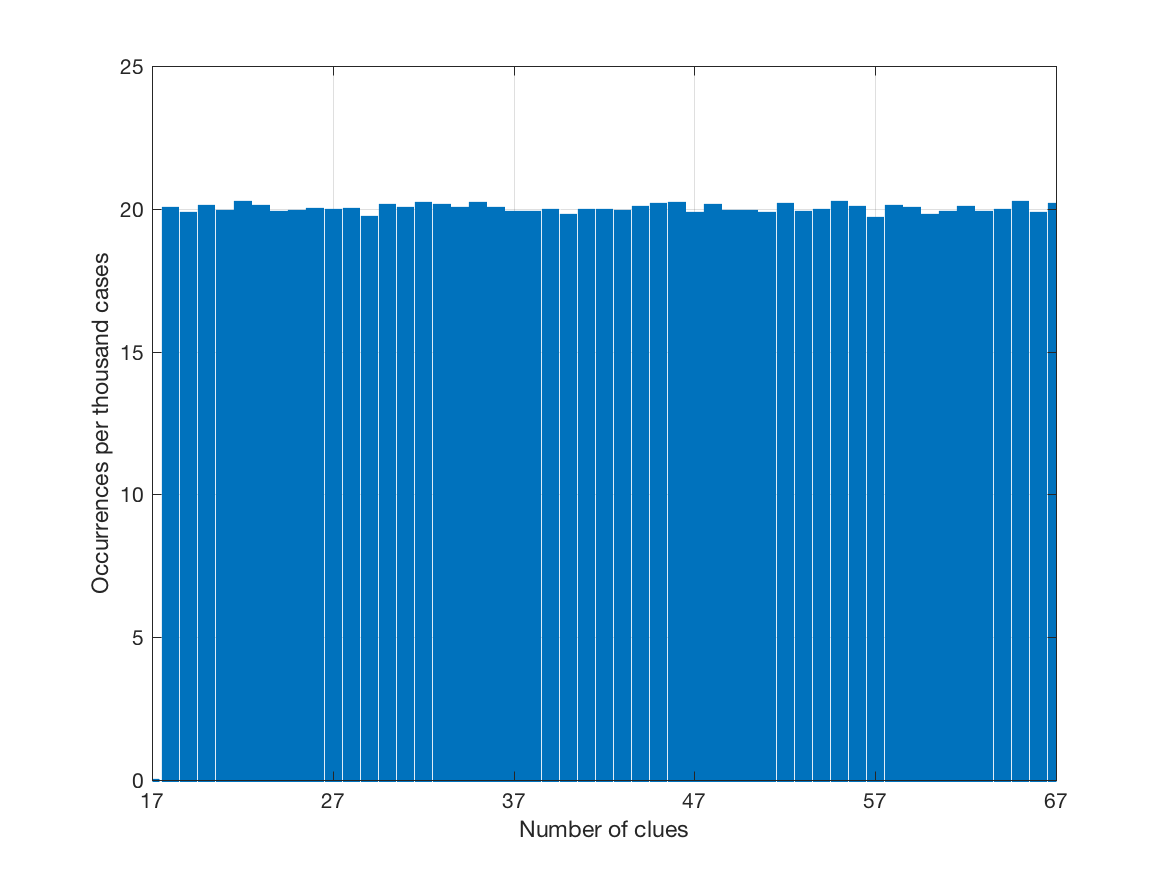
第一个训练数据中题目的难度分布
使用该题集获取训练模型,用时 1 小时 28 分钟,所用算法为 Forward Propagation。该算法的时间复杂度为 O[n^4],参考该文章中的推导。
值得一提的是假如用更多的题目获取训练模型,模型建立和编译的过程尽管会相应延长,生成的文件大小却始终为 91.3 MB,与训练数据的题目数量无关。
测试题目以如下格式存储。共准备了六个题集,存储于目录 ./output/quizzes/,每一个题集中共有 1000 个题目。
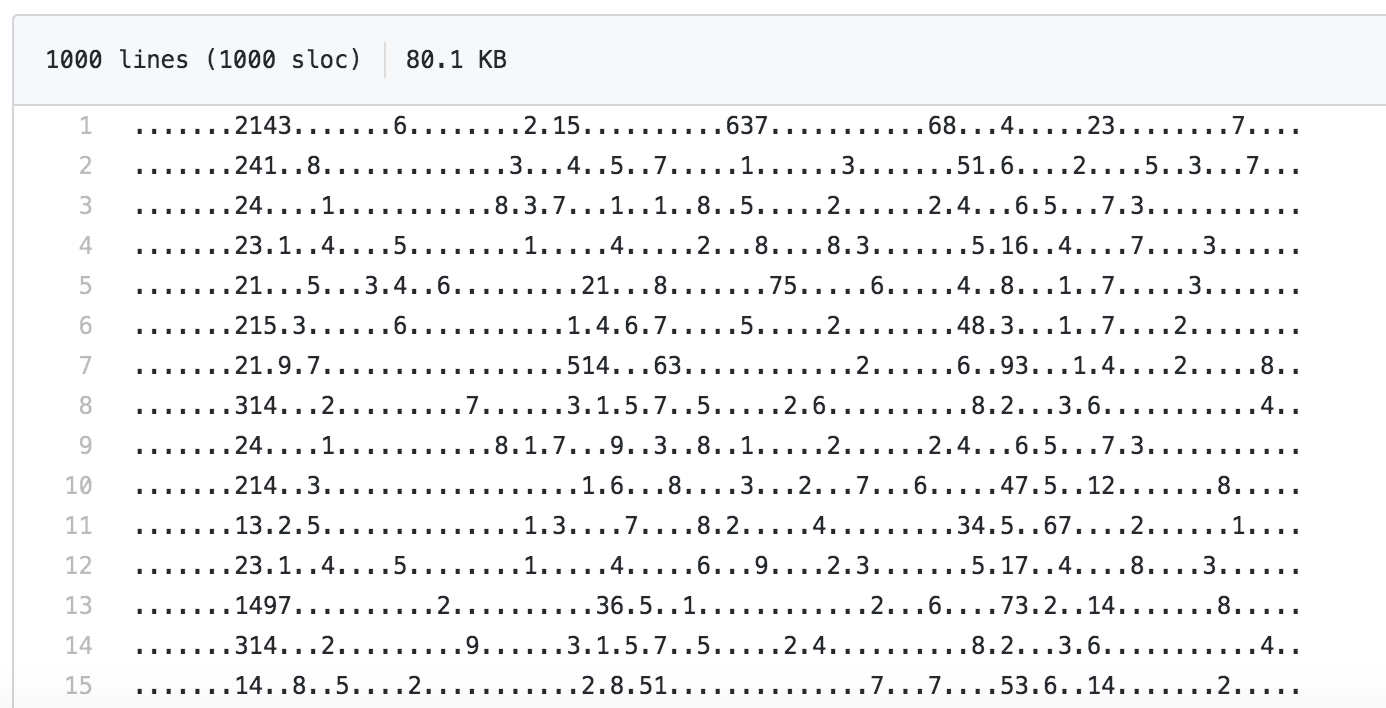
测试题目的前几行预览
前五个题集用与生成训练数据相同的算法生成,第六个题集从这里获 (dao) 取 (yong)。
经过前面的工作,我们有了修改后的 generator.py 核心算法,随机性大幅增加,此外我们简要分析了函数 random.random() 用于生成数独题目的安全性。考虑到梅森旋转算法的周期 2^19937-1 是一个非常大的数字,又由于数独的组合情况非常之多,我们认为用同一个算法来生成测试题目是没问题的。
每求解一千个题目,计算出正确率和总用时,结果如下:
1
2
3
4
5
6
7
8
9
| Level | Clues | Accuracy [%] | Time [sec] |
| -----:| -----:| ------------:| ----------:|
| 1 | 57~67 | 100.000000 | 1.314887 |
| 2 | 47~57 | 100.000000 | 4.958675 |
| 3 | 37~47 | 99.900000 | 20.744941 |
| 4 | 27~37 | 85.300000 | 98.801227 |
| 5 | 17~27 | 52.000000 | 198.944166 |
| 6 | 17 | 39.200000 | 141.365328 |
| Mean | | 79.400000 | 77.688204 |
大体上看,随难度增长,总用时越来越长。这是由于在算法里使用了与人工解题方法相似的策略 —— 每一步仅从神经网络预测的数字中挑选出概率最高的一个填入,再把新的棋盘作为参数重新传入、重新预测。比起一次性预测并填入所有数字来说,这样做的好处是随着填入的数字越来越多,正确率逐渐提高。显而易见,提示数字越少、平均用时越长的趋势也是预料之中的。
最后一个题集 (Level 6) 是制作者精心设计的,不仅所有题目均只有 17 个数字,数字的摆放位置也经过了专门的考究,比我制作的题集里的最后一个困难。我所用的算法没有办法制作这种难度的题目,能做的只有去修改训练题集的难度分布。现做粗暴假设:如果用更难的题目做训练,处理简单的题目至少正确率不会下降。说具体点,如果用一个仅包含难度五的题集来训练神经网络,求解难度从一到四的题集应该也没问题(这是由于简单的题目,可以理解为 “填入了部分数字后的难的题目”,相当于求解过程进展到一半)。
为了实现以上想法,为每一个级别设置了如下专门计算的概率,五个数字的加和为 1,同时满足每一个级别拥有前一个级别两倍多的题目。
1
weights = {5: 0.516, 4: 0.258, 3: 0.129, 2: 0.065, 1: 0.032}
在重新生成的训练题集中,初始数字的分布如下(越难的题目数量越多):
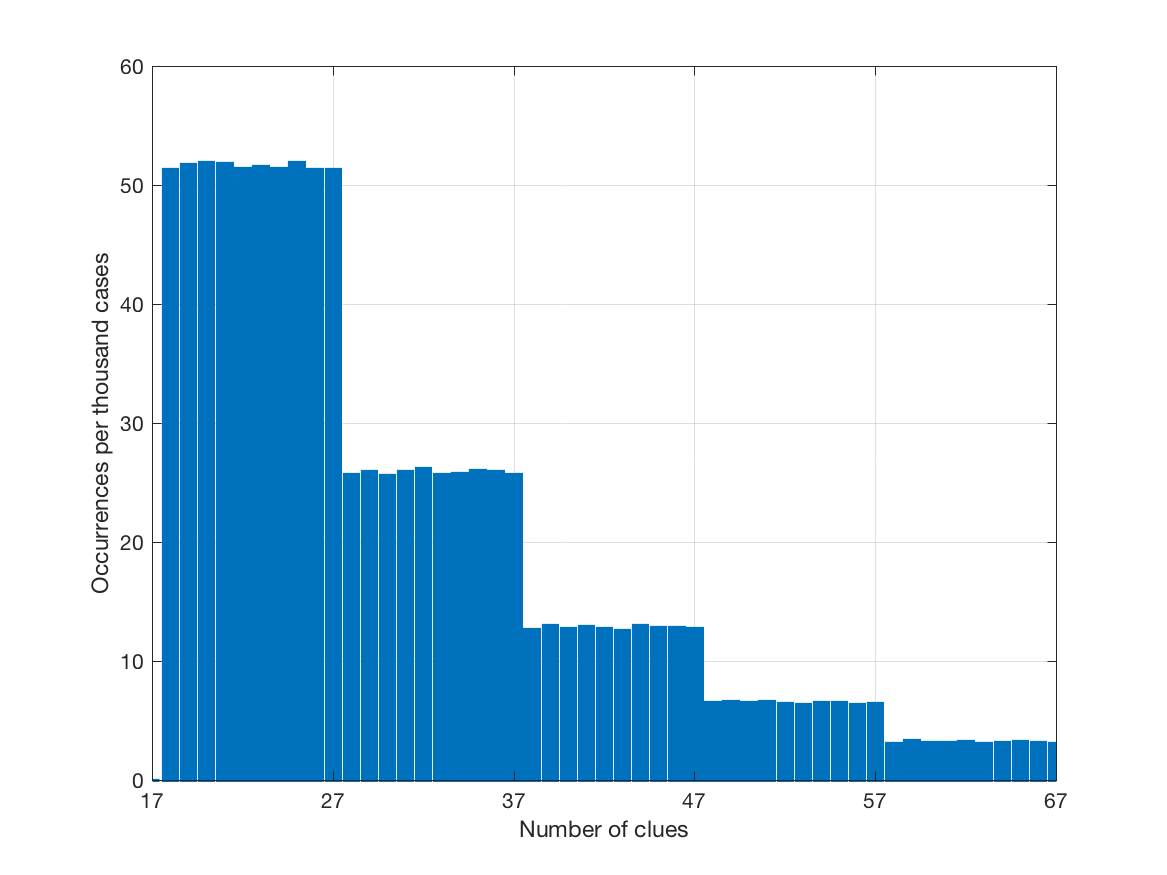
第二个训练数据中题目的难度分布
重测结果中,级别四和级别五的正确率分别增长了 2.0% 和 2.8%,最受关心的级别六的正确率并无增长。级别五与级别六的时间开销都比上一回长,所有级别的平均用时增长了 0.4% - 可忽略不计。从平均的正确率有 0.6% 的提升看来,对训练数据改变难度分布到底还是起了点作用。
1
2
3
4
5
6
7
8
9
| Level | Clues | Accuracy [%] | Time [sec] |
| -----:| -----:| ------------:| ----------:|
| 1 | 57~67 | 100.000000 | 1.309379 |
| 2 | 47~57 | 100.000000 | 4.919540 |
| 3 | 37~47 | 99.600000 | 20.751100 |
| 4 | 27~37 | 87.300000 | 98.709672 |
| 5 | 17~27 | 54.800000 | 199.757209 |
| 6 | 17 | 38.300000 | 142.685764 |
| Mean | | 80.000000 | 78.022111 |
That being said,比起数独庞大的状态总数 1.96x10^20 来说,仅用一百万题集的小样本获得了 80.0% 的正确率,平均用时不差于本文所讨论的其它算法… 尽管训练模型的建立 + 编译过程比较漫长,考虑到以上优点,深度学习的综合表现是不错的。
—— 性能测试 ——
为本文所有方法做一个性能测试,两道测试题目的难度分别为简单和中等,其结果如图。组合搜索法 (Permutation Search) 的 CPU 核心数目由 multiprocessing.cpu_count() 算出。
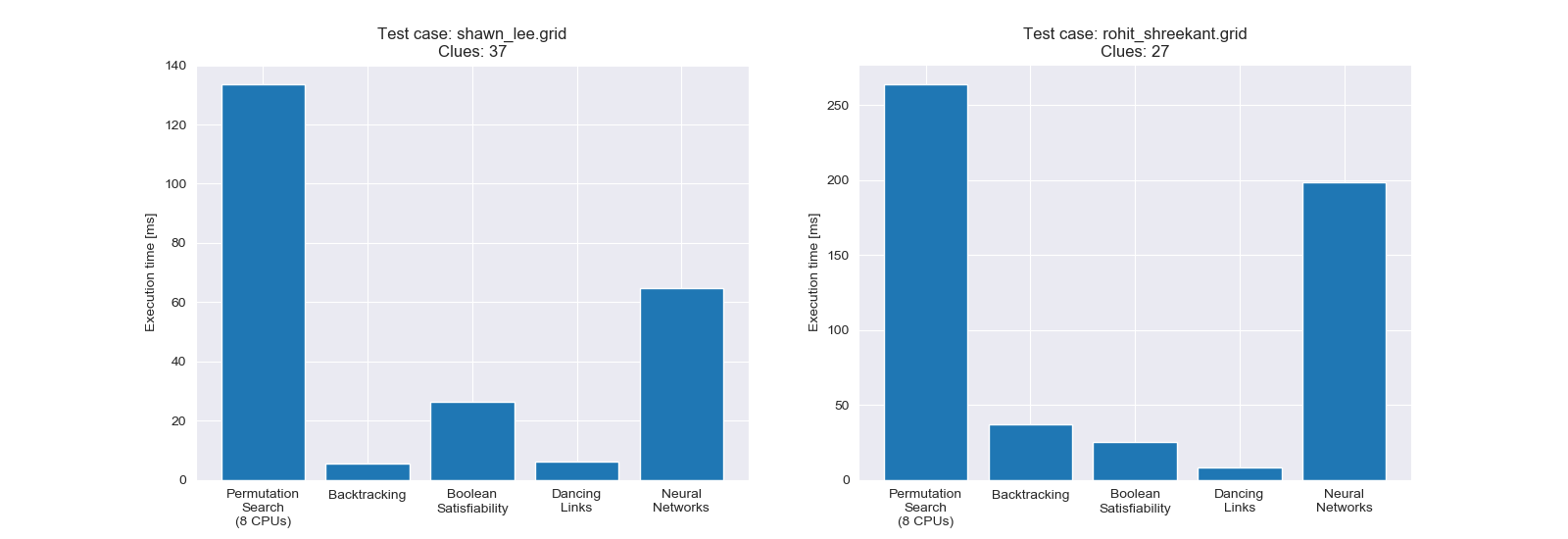
本文所有方法的用时比较
组合搜索法当中,CPU 核心数对运行时间的影响,所选测试题目难度为中等(该题目有 254 个合法的解,在多解数独当中属罕见情形):
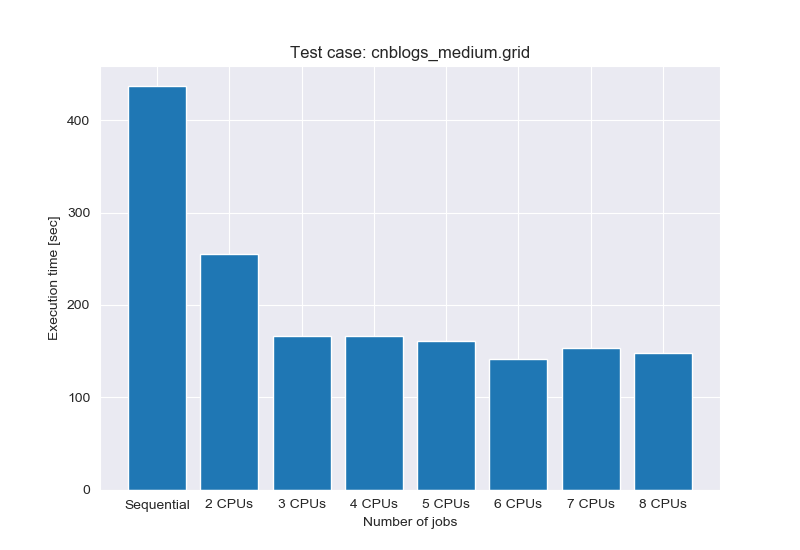
CPU 核心数目对运行时间的影响
Python 3 里,在上下文管理器环境中使用计时函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import time
class Timer:
def __init__(self, func=time.perf_counter):
self.elapsed = 0.0
self._func = func
self._start = None
def start(self):
if self._start is not None:
raise RuntimeError('Already started')
else:
pass
self._start = self._func()
def stop(self):
if self._start is None:
raise RuntimeError('Not started')
else:
pass
end = self._func()
self.elapsed += end - self._start
self._start = None
def reset(self):
self.elapsed = 0.0
@property
def running(self):
return self._start is not None
def __enter__(self):
self.start()
return self
def __exit__(self, *args):
self.stop()
print('Elapsed time is %f seconds.\n' % self.elapsed)
几种不同的使用方法:
1
2
3
4
5
6
7
8
9
10
11
if __name__ == '__main__':
t = Timer()
with t:
pass # running something
with Timer() as t:
pass # running something
with Timer():
pass # running something
参考资料有点儿多,存了好几个子文件夹的东西,仅列举正文中提到的几个吧!
- Chiu, A., Nasiri, E., & Rashid, R. (2012). Parallelization of sudoku. University of Toronto December, 20.
- Harrysson, M., & Laestander, H. (2014). Solving Sudoku efficiently with Dancing Links.
- Karp, R. M. (1972). Reducibility among combinatorial problems. In Complexity of computer computations (pp. 85-103). Springer, Boston, MA.
- Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. science, 220(4598), 671-680.
- Nicolae, I. D. V., & Nicolae, A. I. P. (2012). Limiting Backtracking in Fast Sudoku Solvers. Annals of the University of Craiova, Automation, Computers, Electronics and Mechatronics, 9(36), 25-32.