本文所用方法一览:
- 组合搜索法(多进程)
- 整数规划(单纯形法)
- 布尔可满足性
- N 皇后解法
- 精确覆盖解法
- 神经网络预测法(试验版本)
部分方法详解,其它仅作介绍。
—— 前言 ——
作为科班出身的 Computer Scientist,我一直希望以过来人身份澄清一些看法,谈一谈程序员之间怎么拼内功。换一个方式来讲,我 CSers 固然都是写代码的,你地球物理学家也算是写代码的,此 “编程” 与彼 “编程” 有何本质上区别?我系某大牛(张佳)相信 “地球物理学家能当程序员使”,用来回答 “地球物理专业学完是不是能当半个 CS 使?” 这个问题。无论其依据何在,这听起来似乎有点离谱。
这么多年下来,据我观察,这位大牛之所谓 “编程” 其实也就是大众化的水准,没看出比周围人多会多少。恕在下直言一点事实,不带有任何偏见:学了这么多年,没感受到有多少相同的地方,稍微经过一点点调查的人都不会得出这种结论来。毫不留情地说,在这个系或这个专业里,大多数人算法与数据结构还没入门,何谈 “当程序员使”?恕我直言,CS 专业的作业题以地球物理的方式来写,有一多半都过不了运行时间的限制。恕直言,地球物理这个专业的人想从事跟编程相关的工作,还得从基本原理开始学起!
你明明不懂,还这么骄傲……
—— 基本理论和性质 ——
开博第一篇,先跟大家交待自己的学习背景。
在加拿大攻读计算机科学辅修学位,翻看过数学家 Kenneth H. Rosen 的数论教材,研究过包括 SICP 在内的计算机科学经典教材并因此而学了函数式编程(强制你形成递归的思维),见识过各种各样牛逼的解题方法… Common-Lisp, Java, Python… 是我那时为了读算法书而学的。知道这个圈子的水有多深,对于这个领域内的各种出题套路和比赛规则,我都稍有了解。看到一些周围的人说自己 “喜欢编程”(如:张佳和吴果)而没有体现出足够的热情,我总感觉不够中肯、对自己评价太高。
普林斯顿大学教授的神作(鄙人在加拿大时,这本书已经出到第四版,也是目前的最新版)
如果说要学好一门技能,九成靠的是钻研和自学,那往往这 10% 的启发和引导是最重要的。我那时所接触到的程序设计方法对我至今影响深刻,尽管这些训练只能让我成为一个新手,好在我走的是以算法为核心的正规化学习路线。Computer Science 如同纯数学,有推导有结论,是一门理论性很强的研究型学科。大多数国外大学的 CS 专业会把教学精力集中于算法,编程语言作为工具,需要你自己去学。外行人眼中 “CS 专业的人会用的编程语言比我们多” 之理解,描述的是一种表象、一种衍生的效果。
在我看来,ACM 一类的比赛尽管脱离实际的项目开发,对于大学生的算法设计能力是一种良好的训练。算法是软件的基本单元 —— 不同人员开发的代码借由 API 相互调用、协同运作,只有当每一个部件都优化到位,才能将整体的性能发挥到极致。考虑到硬件的更新速度赶不上数据量的增长,从这个角度来说,算法比赛和研究的意义始终不容忽略。我虽代表不了这个学科的最高水平,希望以数独为例,引出算法比赛里的一些经典而巧妙的优化方法与解题思路。
所以你确定自己真懂?
为了更好地解释后文要讨论的 CNN 训练数据生成问题,就不得不提数独的基本性质。简要总结,有以下这些:
- 至少有 17 个提示数字(的标准数独)才可能有唯一解;
- 把一个填好的数独中所有的 1 都替换成 9、所有的 9 都替换成 1 后,得到的仍然是合法数独(其它数字同理);
- 棋盘整体旋转 90 度不破坏一个数独的合法性;
- 交换同一区域内的两行或两列不破坏合法性等等。
数学家为了尽可能节省用计算机验证 “仅含 16 个提示数字的数独不可能有唯一解” 的计算量,发现了如上规律,并将该定义下等价的数独集合称为等价类。数学中有着各种各样的群,数学家花了大量的精力来对这些群进行分类。最简单的分类之一就是连续群和离散群,而群论就是通过群这种抽象结构来研究种种对称性的数学分支。由于数独存在这样的性质,就可以把经变换后等价的数独归纳为同一类处理,需要处理的数独数量从 9!x722x27x27704267971 减少到 5475730538。
在利用计算机来验证离散数学问题时,归纳排除是一种强大的手段。2010 年,利用谷歌提供的高性能计算资源,Kociemba 等人宣布了还原任意状态彻底打乱的三阶魔方的最小步数,所用分析手段之一是对三阶魔方的对称性和集合覆盖进行一番整理。四色定理的验证也使用了一定的归纳方法,否则在有生之年无法穷尽所有组合。
推荐阅读
无论是求解组合问题还是编写棋类游戏的 AI,暴力搜索都是一种不值得推荐的做法。为了节省篇幅,希望跳过穷举法的实现细节,直接讨论比穷举法稍快一点的数独求解方法 —— 组合搜索法。
所谓暴力穷举,一般是枚举每一个空格内的所有可能 O[N^3] 或枚举每一个 3x3 宫格内的所有可能 O[N(N!)],两种解法的时间复杂度一目了然。第一种穷举法的判断次数比数独的状态总数还要多,第二种穷举法尽管因避免同一宫内数字重复的情况大大减少了判断次数,约束条件还是不足。虽然对小的问题,穷举法也是几秒给出答案、与高级算法差距不大,问题稍大就会增长很快。所以既然下定决心要研究这个问题,就不要使用这种上个世纪就被淘汰了的做法。
为了对穷举法进行改进,可以在九个宫格做全局的循环以前,先把他们每三个组合在一起(组合搜索法),整个棋盘形成上、中、下三个区域。每个区域的三个宫格先进行组合,筛选出局部合法的解(也就是水平方向不能有重复数字),将它们缓存在变量里,再用三个区域的合法解的集合做全局判断。
1
2
3
4
5
6
7
8
9
10
11
12
13
# * ----- + ----- + ----- *
# | | | |
# | 0 | 0 | 0 |
# | | | |
# * ----- + ----- + ----- *
# | | | |
# | 1 | 1 | 1 |
# | | | |
# * ----- + ----- + ----- *
# | | | |
# | 2 | 2 | 2 |
# | | | |
# * ----- + ----- + ----- *
组合搜索法的区域划分方式
写到这里,你或许以为穷举法已经没有优化的潜能了,其实不然。你还可以采纳以下策略进行加速:(1) 三个区域的解组合前,先做一个排序,把解的个数少的放在外层;(2) 前两层循环的里面、第三层循环的外面加一个判断,如果前两个区域的解组合后已经有纵向重复的数字,直接跳过第三层循环;(3) 使用多进程(Python 里请自觉使用多进程,因为多线程对加速无用,下同)。
对于提示数字个数为 17-21 的数独,每一个子区域可组合出的解的个数在 1800 到 4500 之间,全局的总判断次数终于缩小到 1.94x10^10 这个量级。估算运行时间恐怕比较困难,实际跑起来看,在现在的 i5 处理器上用 8 个进程仍需等待 2 分 28 秒。尽管也不算漫长,距离大多数算法比赛规定的时间限制还是相差太远。尽管我们已经绞尽脑汁想尽各种办法来做优化,穷举法写出来的程序肯定超时,这种做法也会让编程求解数独失去研究价值。
除以上智商不低于 80 的人都能想出来的解法,还有以下这些高级解法:
- 模拟退火法 [Kirkpatrick et al., 1983] - 非线性反演问题的通用算法,目前为止求解数独最不靠谱的方法(主要在于成功率)。除了在超高阶魔方中有个应用,2013 年由中国科技大学陈希发表在【高性能计算与应用】上面,一般来说组合数学问题不会选用这种方法。
- N 皇后解法 - 当年在作业题里遇到过很多,在 CS 专业应该属于简单问题。N 皇后是经典的回溯法例子,也是一个 NP-hard 问题。作为对八皇后问题的扩展,N 皇后问题求解的是在 N*N 的棋盘上,有 N 个皇后需要放置,需满足任意两个皇后不能位于同一行、同一列或者是同一对角线上,求一共有几种放置方法。
- Dancing Links (DLX)、X 算法、舞蹈链、精确覆盖解法… 名字有很多,说的都是同一个方法。区别在于舞蹈链是从实现角度来说的,精确覆盖是对问题本身的描述。发明人 Donald Knuth 为图灵奖得主、TeX 排版系统创始人、《计算机程序设计艺术》书作者… 在算法界为神一样的存在。没学过数据结构的同学实现这种方法会比较吃力,许多算法问题实际上是寻找最优数据结构的问题。选择或设计了适用于该问题的数据结构,能在规定的时间内跑过也就顺理成章了。
- 其它很值得推荐但不做详细展开的解法:Integer Programming(把数独约化为线性规划问题,再使用单纯形法求解)、Boolean Satisfiability(把数独约化为逻辑电路问题)……
布尔可满足性,也称逻辑电路问题,是最早被证明具有 NP-完全性的问题 [Karp, 1972]。利用这种优化策略,Gist 上某数独求解代码将 CNF 公式的项数减少到

并可以进一步优化成

看到这种摸不着边际的公式兄弟们作何感想?不带一个积分符号、微分算子,小学生都能看懂,要想推导出它们却不能只用初等数学知识… 数论书里到处都是这种惊艳的结论。
带入标准数独的行列数 n=9,以上两式分别得 11988 和 10530。相比于穷举法要快很多自不必说,甚至,这种解法的效率并不比后面要讨论的舞蹈链低。
所以,从当前的方法下手多思考如何改进,总比靠硬件方法来加速更有研究价值。真想提速的话,用 C++ 重写所获得的效率提升都比用多进程明显。某些情形下,还得考虑进程之间的数据共享,搞不好依赖关系,容易出大问题。经验表明:假如一块 CPU 拥有 1024 个核,1024 个核同时工作,获得的效率提升远没有 1024 那么高。能有核数量的三分之一就很不错了,况且数据量的增长速度永远要比核心数的翻倍速度更快。优秀的算法给你带来革命性的变化 —— 从 60 秒缩短到 2 秒、从 2 秒缩短到 10 毫秒… 如此级别。
退一步讲,实际情况中要不要使用多进程,一来看数据结构和所要解决的问题,二来即使是可以被加速的情形,也要在效率、内存占用… 等问题最大程度上被优化的前提下才可以考虑,而不是一上来就想着用硬件方法。下面再详细解释第一点。
- 何为 “看数据结构”?红黑树或者 AVL 树、走迷宫与求解数独用的回溯法… 数据结构或算法本身决定了可以使用多个分支搜索,并且我们知道正解存在于某一个分支上。这样一来,只要在一个进程上找到答案,所有的进程同时被终止,可以最大程度上发挥多进程搜索的好处。同时也减小因运气好坏而带来的差异 —— 无论正解在哪个分支,用时相差不多,无所谓 good or bad cases。
- 何为 “看所要解决的问题”?最短路径、Hamilton 回路… 虽然也可以采用多个进程搜索、实现加速效果,但是在所有进程都执行完以前无法判定哪个是最短路径、是否不存在 Hamilton 回路… 这一类问题,这是由问题本身的性质决定的。上述回溯法中,如果把问题改成 “八皇后有多少个解”,就不可以在一个进程搜索到答案后终止所有进程。
- 还有一些更棘手的例子,如快速排序,如果不采用并行的思想重新设计,很难有显著的效率提升;平衡二叉搜索树 (Balanced BSTs) 是一个典型的核越多、速度越慢的例子,除非是采用分治方法 (Divide-and-Conquer);从底往上形成节点的 Huffman Tree 也很难写成多进程版本,原因不用说也明白。
考虑到以上这些限制,算法比多进程拥有更大的应用范围和更直接的效应。假如在某种情形下我可以用 (1) 多进程和 (2) 更好的算法,我优先选择用算法来加速。算法方面的基本功不仅决定了你可以成为哪个档次的开发人员,更是资深程序员用来显示逼格的一种资本。
—— 实现细节 ——
以下所有讨论,均假设初始状态的数独拥有 17 个提示数字。仿照 LeetCode 上面的要求,规定每一种方法的运行时间不得超过 150 毫秒。不装逼,装逼遭雷劈,许多算法比赛里的编程题,题目看起来白痴,难就难在需要在规定的时间内跑完。
【N 皇后解法】 —— 原理不难理解,能充分发挥多进程的优点,多解情形只能给出一个答案
在 CS 这个学科里面,几乎哪里都离不开深搜遍历,这种算法几乎是万能的。求解数独问题,虽然不需要使用树型结构,在 N 皇后/回溯法里面依然体现了深度优先搜索的思想。

八皇后的一个两步解法,所用策略为最小冲突
用摆 N 皇后的方法破解数独,可以遵循以下流程:
- 定义一个函数
n_queens(),它读取一个代表数独的多维数组grid,根据一定规则选取一个空格子,生成一个数字填入(规则如下条所述),得到一个含有 17+1 个提示数字的新的数独;将此数独作为参数传递给同一个函数,由此形成n_queens()自我调用的递归过程;以此类推,递归每深入一层,初始数字的个数增加一个、空格减少一个… 空位置的选择,关乎全局效率,下文详述。 - 定义一个函数
lst_candidates(),从给定的一个空位置出发,搜索其所在行、列和 3x3 宫格,排除已存在数字后,生成合法数字列表,所填数字从这个合法数字列表中选择。由于这个候选数字列表是随着递归深入逐层计算出来的,所以比穷举法高效很多。 - 在每一层递归中,由于填入的初始的数字不具有足够的约束,它有多种选择并很有可能是错的;当递归达到一定深度时,程序经判断得出没有可填入数字了,则返回到上一层,更换数字后再次尝试;如果上一层所有候选数字都已经尝试过了仍然无解,则继续返回上上层尝试新的候选数字。
- 在经过了一番尝试之后,当递归达到最深一层(即整个棋盘被填满后)并无遇到冲突,则说明前面填过的所有数字都是正确的,该程序返回结果。
不难看出,如果给 n_queens() 传递一个全是 0 的 grid,很容易将回溯法改写成一个随机生成数独题目的函数。
剪枝优化问题
为了更好地解释这个问题,先定义 peers 是什么。所谓 peers 就是与某个空位置在同一行、同一列和同一宫格内的所有其它格子(已填数字的格子也包括),定义完毕。为了有效地缩短候选数字列表,减少搜索分支,引入如下法则,英文里叫 Constraint Propagation:
- Rule I: 对于每个空的位置,peers 里的已存在数字需要排除,得到一个候选数字列表。通常这样做后仍然无法确定该空格内数字。
- Rule II: 如果某一个空位的所有 peers(包括已存在数字)都有某个特定数字被移除,那么这个空格必须填入那个缺失的数字;一旦确定,该空格成为 singleton(注意 Rule I 有时也能确定 singletons),即只有唯一可能。
不难得出以下两点推理:
- Rule II 最多只能返回一种可能,即不可能有两个以上数字同时从所有 peers 中移除。
- Rule II 所确定的解答必从属于 Rule I 所提供的可能。
根据以上法则,设计一个算法,程序开始前先用 Rule I 和 Rule II 交替搜索,找到尽可能多的 singletons;每填入一批,对棋盘重新搜索,又会有新的 singletons… 直到没的填为止,再用核心算法(回溯法、穷举法…)求解。通常对于简单的数独,在经过几番这样的搜索后棋盘已经填满;有些难的数独数字摆放经过了特殊的设置,用这个算法就找不到任何 singleton。
函数 lst_candidates() 的定义有多种实现方法。
第一种方法(即时触发型),给定参数 grid(代表一个 9x9 数独)和坐标 (i,j),根据坐标搜索其 peers 里已存在数字,生成如下数组:
1
2
3
4
5
6
7
8
def lst_candidates(grid, i,j):
"""lst_candidates() 初等写法"""
# enumerate existing clues
filled_row = []
filled_col = []
filled_box = []
# 此处略去一些代码
return candidates
再用 Python 自带类型 set() 计算三个数组的并集。这种方法,相信是没怎么考虑优化的同学首选的版本。这种策略效率很低,有以下几点原因:
- Rule I 是 Rule II 的 dependency,为判断某一个空格是否 singleton,需要对其每一个 peer 进行这样的检查,造成对
lst_candidate()的重复调用。 - 即使只用 Rule I,在对整个棋盘遍历列出每一个空格的候选数字时,也会对列、行、宫造成重复性搜索,这是因为每行、每列、每宫通常会有多个空格。
- 初始状态的数独一般比较稀疏,0 的个数多于提示数字的个数。这种方法只有当遇到非零数字时才进行存储,再分析下一个格子,所以效率很低(可以考虑用
numpy进行向量化,不必逐个分析)。
既然这种搜索方法效率很低,不妨在每层递归只做一次这样的搜索,将已存在数字以索引的形式缓存成字典,参考稀疏矩阵的存储方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
def cache_clues(grid):
# enumerate existing clues
# ...
return clues_row, clues_col, clues_box
def lst_candidate_fast(clues, i,j):
clues_row, clues_col, clues_box = clues
# 通过格子坐标 (i,j) 计算出 box number (m,n)
filled_row = clues_row[i]
filled_col = clues_col[j]
filled_box = clues_box[(m,n)] # 再用索引快取
# 此处略去一些代码
return candidates
同理在用 Rule I 进行搜索后,将每一个空格的坐标和候选数字成员用字典或多维数组存储,坐标充当索引,供 Rule II 使用。归功于哈希函数,Python 里用键值访问字典提取信息只需要 O(1) 时间(存在争议)。反正内存那么大,留着做何用?这种道理,是作为程序员用空间换取时间的最基本方法,就连刚接触数据结构的本科生都懂。
通过位运算提高效率
回溯法比穷举法效率高的一个原因,就是可提升空间更大、可进行优化的地方很多,剪枝优化就成了一个影响效率的关键性操作。如果把估算优先权的算法写得过于详细,如:把后面几层的候选数字列表全预测出来,剪枝效果确实做到了极致,却花费了太多时间用于预判上面,得不偿失。由于递归每深入一层,需要遍历整个棋盘,找出候选数字最少的空格,造成对 lst_candidates_fast() 子函数 cache_clues() 的重复调用。函数 cache_clues() 的实现方法必须设计得非常精巧,这个函数的效率关系到总体的性能。
我们可以进一步设计一个 cache_clues_bin() 版本,采用二进制进行加速。先把 1-9 九个数字用一套规定的二进制表示展开,如下:
1
2
3
4
5
6
1 = 000000001
2 = 000000010
3 = 000000100
4 = 000001000
…
9 = 100000000
在分析每一个空格子过程中,将 peers 里已存在的数字转换成二进制,取反后与 111111111 做一次 AND 运算。比如,搜索过程中遇到了 7 = 001000000 这个数字,7 的二进制取反后得 110111111,与 111111111 做一次 AND 运算后得 110111111,那么这一串字符中就包含有候选数字列表的长度与成员的信息。对于二进制整数,有一种非常高效的算法可以快速计算所含 1 的个数。
由于二进制运算的高效性,这种算法在遍历整个棋盘、枚举每一空格候选数字的同时,或许还能进一步缩短时间(使用位运算是算法里面常见的装逼手法之一)。
一个函数 lst_candidates() 就有这么多种优化方法。只有你想不到的,没有做不到的。
【精确覆盖解法】 —— 目前为止效率最高、实现难度最大的数独求解算法,需要学习的东西很多

一个精确覆盖问题的图论表示方法,转自维基百科
乍看起来,这幅图似乎和数独就没有什么联系,其实数独和精确覆盖问题有一种精妙的等价关系,这种不太直观的联系是由算法科学家出面解决的。只要对应的精确覆盖问题得解了,数独也就得解了,这在信息学里是一种常见的向上约化现象。这种约化的目的是为了保证数独里每一行、每一列还有每一宫格都满足精确覆盖的解。

一个由数独转化成的精确覆盖问题(该矩阵有 324 行、729 列)
不只是数独,其它 CS 里面的组合问题也都是通过约化为精确覆盖问题求解的,如五格骨牌:
一个 8x8 的 Pentomino,转自维基百科
想要用精确覆盖问题的方法求解数独,你需要学习的要点有:(1) 什么是精确覆盖问题;(2) 如何把一个数独转化成精确覆盖问题;(3) 精确覆盖问题如何求解。前两个似乎不难解决,但是与 N 皇后的算法相同,精确覆盖问题的算法套路也包括递归和回溯两个步骤。在矩阵的某些行被删掉之后,你如何复原一个初始的矩阵?为了不破坏原始矩阵,需要在内存中生成大量拷贝。若不能很好地解决这个问题,用这种方法编写出来的程序效率可能比穷举法还低。
Donald Knuth 为了高效地解决这个问题,发明了舞蹈链这种数据结构,基本原理是双向链表。用这种数据结构实现的算法,递归过程中不占用额外的内存,回溯效率惊人。

一个精确覆盖问题的二进制(左)和舞蹈链(右)表示方法
链表是除数组以外最先需要考虑的数据结构,也是算法设计中最基本的加速方法之一。双向链表当中,每一个成员包含一个值和两个指向相邻成员的指针(Python 里没有指针,请使用 attribute,下同)。如有需要,可首尾相连形成环状结构。当某一成员需要执行“被删除”操作,只需修改前、后两成员的指针使得这个“被删除”成员在遍历时被跳过,便于对已删除的数据进行快速恢复,因而更适合需要频繁增减的情境。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import collections
class Node(object):
"""双向链表节点"""
def __init__(self, data):
self.item = data
self.nref = None
self.pref = None
class DoublyLinkedList(collections.Sequence):
"""双向链表"""
def __init__(self):
self.start_node = None
def is_empty(self):
return self._head == None
def __len__(self):
pass # 此处略去一些代码
def add(self, item):
pass # 此处略去一些代码
def append(self, item):
pass # 此处略去一些代码
def search(self, item):
pass # 此处略去一些代码
def __str__(self):
pass # 此处略去一些代码
类似地,我们可以将所有相邻节点连接起来,形成四路链表。舞蹈链(又称十字链表)是双向链表的升级版,每一个成员包含一个值和指向相邻四个成员的指针。
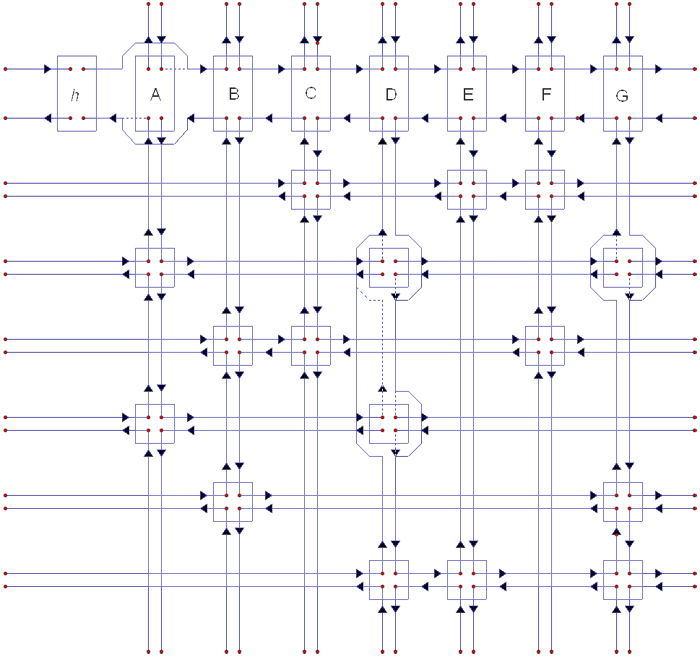
从舞蹈链当中删除和复原节点,转自 medium.com
舞蹈链的提出和应用把原本需要两分多钟运行的东西变成了十毫秒,无论多难的数独都可以在瞬间解决。即使对一个数独都有如此明显的效率提升,何况是拥有上亿数据量的大型工程问题?无疑,这是目前为止 “编程求解组合问题的最高境界”。
把问题化繁为简,可以遵循以下步骤实现:
- 编写一个求解一般的精确覆盖问题的程序,与例题结果进行对照
- 编写将数独转化为精确覆盖问题(及其逆转换)的程序
- 用第一步实现的代码来求解数独转化成的精确覆盖问题
呼… 要想真正高效地求解一个数独问题,所需要的知识还挺多的!在我看来,这些数据结构非得要亲自实现一遍才能叫基本功过硬,这也是为什么很多人到了大二就放弃了。在滑铁卢大学读 CS,平均成绩只要够 80 就可以去 MIT 上研究生。全世界唯一一所享受如此待遇,可见其评分制度之严格。来到这里,各路算法比赛的大神居然会有 “觉得自己基础太差”、“读着吃力” 这种感觉… 何况是我等普通人?
“上 CS 被虐” 与 “打 CS 被虐” 到底哪个更惨烈一些?都挺惨的!只是倒下的姿势不同而已……
可见编程其实并不好学,主要难在:(0) 选用什么样的数据结构,在缺少背景知识的前提下,仅凭临场发挥很难构思出来(思路难);(1) 有些算法基本原理已经非常难懂,更别说亲自实现出来(实现难)。后者通过刷题可以逐渐克服,前者决定了你能否回答面试官问题。这个世界每时每刻,各种烧脑的算法被大牛们创造出来。即使翻过了世界上每一本算法书,还是会有你答不上来的问题,并且在地球物理这个专业几乎没人思考这些。
所以依我看,CS 到底还是跟组合与优化、数理逻辑、群论、数论和图论联系得更紧密一些。
我想起来一篇文章……
【神经网络预测法】 —— 实现过程只需入门水准,深入探讨会有些复杂,求解效率与其它高级方法不相上下,正确率有待进一步提高
(接下)

